Public transport
The public transport model is an allocation of passengers to public transport lines, such as train, metro, tram and bus. An important aspect of the model is also the first and last mile of transport: the way you travel to and from the public transport stop (access and egress, respectively). The model decides how people travel to a public transport stop, which public transport lines they take to their destination stop, and which mode they use to travel from the destination stop to their final destination. The model can be used to analyze the use of the public transport system, but also to analyze flows of e.g. pedestrians and bikes traveling to and from public transport stops.
Overview of computation steps
The overview below shows the steps that are used in the public transport allocation model to compute transit intensities.
- Stop selection: a process which selects a subset of stops for each zone in the network.
- Path building: execution of a path search algorithm to compute the travel times between all combinations of stops.
- Trip assignment: for each origin-destination pair the corresponding trips are assigned to combinations of stops.
- Computation of intensities: given the trips assigned to stops, the intensities of the transit lines are computed.
- Write output for visualization.
More details about these steps can be found in the sections below.
Stop selection
The stop selection step is responsible for choosing the stops that may be chosen for a given origin-destination pair. At the origin side a subset of stops is selected, also known as access stops. Similarly, at the destination side a subset of egress stops is selected. These subsets represent the stops the traveler can choose from when departing from the origin zone, and when reaching the destination zone. We illustrate this with an example. When a traveler departs from a house, there is typically a limited number of stops that is considered, depending on the public transport lines that provide service at these stops and depending on the destination. This can be the set of stops that is closed to the house, but typically people also consider special stops such as train stations, even if they require a slightly longer walk or bike ride. The stop selection step should be seen as a preprocessing step that create the subsets of stops, but it does not make the actual stop choice yet.
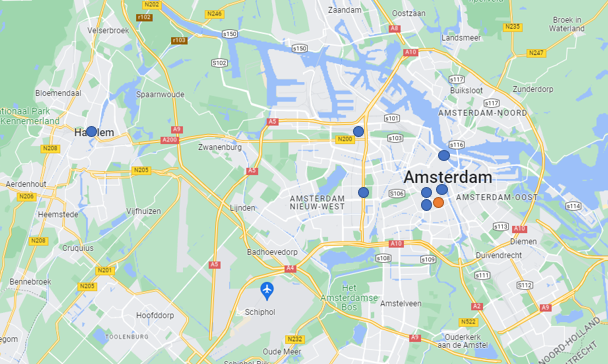
We illustrate the stop selection step with an example, as shown in the figure below. The zone is highlighted in orange, and the subset with selected stops contains seven stops, highlighted in blue. The algorithm always selects the stops within a given radius from the zone, but in addition it also selects additional stops based on the stop type, even if they are outside the radius. This enables the modeler to define that always e.g. a train station should be considered. In the example it can be seen that Amsterdam Centraal, Amsterdam Lelylaan, Amsterdam Sloterdijk and Haarlem were selected. It is important to note that Haarlem station is relatively far away, and most likely travelers departing from the orange zone will not choose it. However, the actual choice is made in the trip assignment step.
Path building
In the path building stage a function \(C(s,d)\) is computed, which defines the cost to reach destination stop \(d\) from each stop \(s\) in the network. The cost is computed based on:
- Travel time
- Waiting time at stops
- Penalty for transfers
- Fare (only available for Dutch networks)
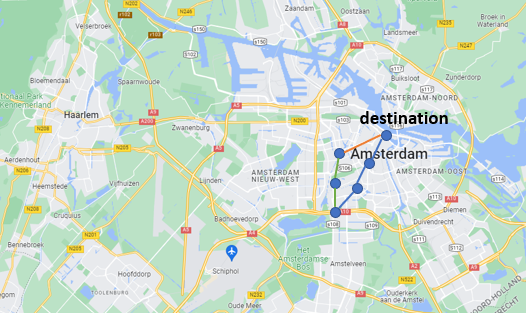
The function \(C\) is computed using a search that starts backwards from the destination \(d\). In the example in the figure the search starts from Amsterdam Centraal (the destination), and it traverses all incoming lines (i.e., the blue and orange line) backwards. During the traversal it updates the function values of \(C\) for the stops encountered. After all incoming lines were traversed, the procedure continues with traversing all new lines that were encountered during the traversal. In the example this would be the green line.
After the path building stage, the function \(C\) can be used to infer paths to the destination. If a traveler enters the public transport system at a particular stop, then \(C\) can be used to determine which outgoing lines are chosen to eventually reach the destination. For this purpose it also maintains some auxiliary bookkeeping, which is not described in detail on this page.
Trip assignment
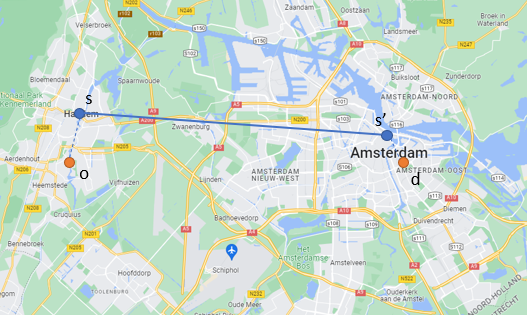
In the trip assignment stage stops are being selected for each origin-destination pair, and trips are assigned to access stops where travelers enter the public transport network. We illustrate this process based on the example shown in the figure below. Suppose a traveler wants to travel from origin \(o\) to destination \(d\). For both zones a subset of stops was determined in the aforementioned stop selection step. The algorithm enumerates all combinations of stops and uses the function \(C\) to find the combination with the lowest cost. In the example this would be access stop \(s\) and egress stop \(s'\), and subsequently all trips traveling from \(o\) to \(d\) will be assigned to stop \(s\), with destination \(s'\). Please note that the actual path is not chosen in this step. The trip assignment only takes care of the choice for particular stops.
In the example one pair \((s,s')\) was selected, but it is also possible to spread the trips over multiple pairs by using a multinomial logit function, which simulates the fact that a group of travelers may choose multiple different stops rather than just one pair.
Computation of intensities
The final step of the assignment computes the total number of trips per line. It takes the trips that were assigned to the stops in the previous step, and it uses the function \(C\) (with associated bookkeeping) to traverse the network forward until the destinations are reached. The algorithm performs a graph traversal and keeps track of an intensity value for each link in the network.
Assignment based on mode chains
The generic process summarized in the previous steps is performed for multiple mode chains. Each such chain fullfils a trip of a traveler from origin to destination, and consists of an access mode, a public transport part, and an egress mode. For example, a mode chain can be (walk, public transport, walk), which means that people walk to their first access stop, from there they take public transport, and they walk from their egress stop to their final destination. If bikes are also considered, then there are four mode chains that can be potentially used by travelers, and people traveling by bike may choose different stops. In the current implementation of the public transport model the entire process is performed separately for each chain. Furthermore, the model also keeps track of walk and bike intensities to and from stops, and the model stores them separately for further inspection after the assignment process ended.
Input collections
In the overview below we show which data collections should be filled when running the model.
| Collection | Description |
|---|---|
| PT_TRANSITLINE | Information about transit lines. |
| PT_NODE_TRANSITLINE | Information nodes visited by transitlines. These nodes correspond to stops. |
| ROADS | Information about roads in the network. This contains all roads in the network, and not just the ones used by public transport. |
| TRAF_NODES | Nodes in the network. |
| TRAF_ZONES | Zones in the network. |
| OD matrices | For the public transport dimension, you have to provide an OD matrix with trips. |
Output data
In the overview below we describe where the output of the model can be found in the data.
| Description | Location |
|---|---|
| Road intensities | Intensities are available in the ROADS collection, and can be visualized in the interface. |
| Travel times and distances | For each origin-destination pair the travel time and distance can be found in the corresponding OD matrix. |
| Access and egress trips | The collections PT_ZONE_TRIPS, PT_STOP_TRIPS and PT_ZONE_CHAIN_TRIPS contain additional information about access and egress trips. For example, it may be used to e.g. infer how many people bike to a specific stop. |
Parameters and settings
In the table below you can find an overview of all parameters that need to be set prior to starting the model.
| Parameter | Data format | Description |
|---|---|---|
| dimensionPT | integer | Public transport dimension |
| dimensionWalk | integer | Walk dimension |
| dimensionBike | integer | Bike dimension |
| accessEgressDimensions | comma separated integers | Dimensions used for access/egress. Currently this must be walkDimension,bikeDimension. If you do not use bikes in your setup, make sure to create a separate dimension for bikes by duplicating the walk network. |
| minFind | comma separated floats | For each access egress dimension: minimum number of stops to add |
| searchRadius | comma separated floats | For each access egress dimension: radius (km) in which all stops are added |
| numIntercityStopsRequired | comma separated integers | For each access egress dimension: number of intercity stops that need to be added during stop search |
| intensityOutputDimensions | comma separated integers | Dimensions used for writing access/egress intensities. If you put walkDimension,bikeDimension then it overwrites the intensities for these dimensions. If this is inconvenient (e.g., when assigning bikes separately with Traffic), then you need to create separate output dimensions for access/egress and put the dimension IDs here. |
| fullSearchDimensions | comma separated integers | Dimensions for which a full search for access/egress stops is performed. Typically only walk and bike. |
| maxTransfers | integer | The maximum number of transfers that people can make while traveling from origin zone to destination zone. If the traveler walks from a stop to another stop, this counts as 2 transfers! This will be fixed later. |
| maxWalkingTimeTransfer | float | Maximum amount of time that a traveler walks from an intermediate stop to another stop, in hours. |
| maxNumStops | integer | Maximum number of stops that will be added for access/egress stop selection. This parameter is mainly for memory allocation purposes. Recommended value: 20. |
| maxWalkOptions | integer | For each stop the module identifies nearby stops that can be reached by walking. This parameter controls the maximum number of nearby stops for which a walk option is added. For example, when set to 5, it adds walk options for the nearest 5 stops. |
| writeReference | 0 or 1 | If 1, then it sets the ReferenceTravelTime values in the OD matrix. This option should only be used when preparing a scenario in which modal split is used. |
| useGPU | 0 or 1 | If 1, then it uses CUDA on the GPU for the assignment, and CPU otherwise |
| requiredStopTypesWalk | list | The list allows you to define the minimum number of stops you want to have in the access/egress options for a given stoptype for the mode 'walk'. The expected format is [ [stoptype,number], [stoptype,number] ]. If you don't want to use such requirements, use an empty list as parameter setting: [] |
| requiredStopTypesBike | list | The list allows you to define the minimum number of stops you want to have in the access/egress options for a given stoptype for the mode 'bike'. The expected format is [ [stoptype,number], [stoptype,number] ]. If you don't want to use such requirements, use an empty list as parameter setting: [] |
| writeSkims | 0 or 1 | If 1, then the module writes travel times and distances after completing the assignment. |
| numStagesGPU | integer | The execution of one of the GPU kernels can be performed in stages, such that x threads are executed in numStagesGPU stages of x/numStagesGPU threads each. These stages are executed sequentially, reducing the total memory usage of the module. |
| weightTime | float | weight >=0 in generalised cost function |
| weightTransfer | float | weight >=0 in generalised cost function |
| weightWaitTime | float | weight >=0 in generalised cost function |
| focusOrigin | integer | If module should only assign trips for specific OD pair, focusOrigin and focusDestination can be set. Should be -1 otherwise. |
| focusDestination | integer | If module should only assign trips for specific OD pair, focusOrigin and focusDestination can be set. Should be -1 otherwise. |
| focusChain | integer | If module should only assign trips for specific OD pair, focusOrigin and focusDestination can be set. If you set focusChain, only a specific chain access-pt-egress is assigned. 0 is walk-pt-walk, 1=walk-pt-bike, 2=bike-pt-walk, 3=bike-pt-bike. |
| debugOrigin | integer | origin for which debug output is shown during backwards search, -1 means disabled. debug output only works when running on CPU. |
| debugDestination | integer | destination for which debug output is shown during backwards search, -1 means disabled. debug output only works when running on CPU. |
| debugWalkOptions | integer | If you want to see the walk options from a given node/stop in the output, you can set a node object ID, and set it to -1 otherwise |
| debugStops | comma separated integers | object IDs of the stops for which debug output is shown (only if origin and destination were provided) |
| transferPenalty | float | transfer penalty in minutes, included in generalized cost function for every transfer. this value can be found in project setup in OT |
| waitFactor | float | scalar applied to the waiting time in the generalized cost function. this value can be found in project setup in OT |
| malusFactorBusTram | float | scalar applied to the travel time of bus and tram |
| lineTypeBus | integer | line type of bus lines, can be found in PT_TRANSITLINE. This value is used to decide when the malusFactorBusTram should be applied. |
| lineTypeTram | integer | line type of tram lines, can be found in PT_TRANSITLINE. This value is used to decide when the malusFactorBusTram should be applied. |
| lineTypeTrain | integer | line type of trains, can be found in PT_TRANSITLINE. This value is used to decide whether a line is BTM or Train when computing tariffs. |
| temperatureAccessChoice | float | scalar to adjust access choice. higher means that people tend to choose access stops with low cost to destination. It is recommended to start low (e.g., 10), and then increase it to a value in the range [100,300]. If you notice that trips get lost, then lower the temperatures. |
| temperatureDestinationChoice | float | scalar to adjust destination choice. higher means that people tend to choose destinations with low cost. It is recommended to start low (e.g., 10), and then increase it to a value in the range [100,300]. If you notice that trips get lost, then lower the temperatures. |
| stopTypeTrain | integer | stop type of train stations, can be found in PT_STOP. Currently not used, so if no type number is available you can also put -1 here. |
| stopTypeMetro | integer | stop type of metro stations, can be found in PT_STOP. Currently not used, so if no type number is available you can also put -1 here. |
| dimensionWalkWalk | integer | OD matrix dimension for walk-pt-walk |
| dimensionWalkBike | integer | OD matrix dimension for walk-pt-bike |
| dimensionBikeWalk | integer | OD matrix dimension for bike-pt-walk |
| dimensionBikeBike | integer | OD matrix dimension for bike-pt-bike |
| intercityStops | comma separated integers | node ids of intercity stations |
| fareScalar | float | scalar value applied to fares, currently used to compensate for fare overestimation. If you do not want to include fares in the utility function, set this parameter to 0 |
| unitMiles | 0 or 1 | If this parameter is 1, then input distances should be in miles. If this parameter is 0, then input distances should be in meters. |
| includeZeroTrips | bool | Can be set to true to include ODs with zero trips in the computation. |
| enforceWalkTransfers | 0 or 1 | If this parameter is 1, then walking links will be added between stops that are spatially close to each other, even if there are no walking links connecting them. |
Example parameter JSON
The JSON below can be used in the parameters key-value set in the store editor to configure the Traffic model. You can use the button in the corner to copy the JSON to your clipboard.
[{"Name":"dimensionPT","Value":17,"Type":1},{"Name":"dimensionWalk","Value":15,"Type":1},{"Name":"dimensionBike","Value":14,"Type":1},{"Name":"accessEgressDimensions","Value":"15,14"},{"Name":"minFind","Value":"3,3"},{"Name":"searchRadius","Value":"0.8,0.0"},{"Name":"intensityOutputDimensions","Value":"15,55"},{"Name":"fullSearchDimensions","Value":"15,14"},{"Name":"maxTransfers","Value":10,"Type":1},{"Name":"maxWalkingTimeTransfer","Value":0.15,"Type":2},{"Name":"maxNumStops","Value":20,"Type":1},{"Name":"maxWalkOptions","Value":"5"},{"Name":"writeReference","Value":"0"},{"Name":"debugOrigin","Value":-1,"Type":1},{"Name":"debugDestination","Value":-1,"Type":1},{"Name":"debugWalkOptions","Value":-1,"Type":1},{"Name":"debugStops","Value":""},{"Name":"phiBoarding","Value":4.0,"Type":2},{"Name":"useGPU","Value":1,"Type":1},{"Name":"writeSkims","Value":1,"Type":1},{"Name":"requiredStopTypesWalk","Value":"[[0,0],[1,1],[2,1],[3,0],[4,0],[5,0],[6,0],[7,0]]"},{"Name":"requiredStopTypesBike","Value":"[[0,0],[1,3],[2,2],[3,0],[4,0],[5,0],[6,0],[7,0]]"},{"Name":"numStagesGPU","Value":100,"Type":1},{"Name":"focusOrigin","Value":-2076,"Type":1},{"Name":"focusDestination","Value":-92,"Type":1},{"Name":"focusChain","Value":-1,"Type":1},{"Name":"weightTime","Value":"1.0"},{"Name":"weightTransfer","Value":"1.0"},{"Name":"weightWaitTime","Value":"1.5"},{"Name":"transferPenalty","Value":5.0,"Type":2},{"Name":"waitFactor","Value":0.5,"Type":2},{"Name":"malusFactorBusTram","Value":1.15,"Type":2},{"Name":"lineTypeBus","Value":5,"Type":1},{"Name":"lineTypeTram","Value":4,"Type":1,"Unit":""},{"Name":"lineTypeTrain","Value":1,"Type":1},{"Name":"temperatureAccessChoice","Value":300.0,"Type":2},{"Name":"temperatureDestinationChoice","Value":300.0,"Type":2},{"Name":"stopTypeTrain","Value":1,"Type":1},{"Name":"stopTypeMetro","Value":2,"Type":1},{"Name":"dimensionWalkWalk","Value":231,"Type":1},{"Name":"dimensionWalkBike","Value":232,"Type":1},{"Name":"dimensionBikeWalk","Value":233,"Type":1},{"Name":"dimensionBikeBike","Value":234,"Type":1},{"Name":"intercityStops","Value":"987121,900239,900241,900237,900284,900287,900230"},{"Name":"numIntercityStopsRequired","Value":"1,3"},{"Name":"fareScalar","Value":0.2,"Type":2}]
Literature
For more details on optimal strategies and supernetworks please refer to
Spiess & Florian (1989). Optimal Strategies: A New Assignment Model for Transit Networks,Transportation Research Part B: Methodological. 23. 83-102. 10.1016/0191-2615(89)90034-9