Traffic Assignment

Index

About
Data requirements
Model architecture
Methodology
Benchmark

About

The TrafficAssignment model enables to interactively explore the impact of infrastructure changes on the route choice of all road-bound vehicles such as cars, trucks and cyclists. The routes are determined based on travel time and cost factors.

The following interventions are possible with the TrafficAssignment model:

Road speed

Alter mode-specific speed of a selected link of the network.
Road capacity

Alter mode-specific capacity of a selected link of the network.
Turn delays

Alter the delay of turns in the network.
New links

Draw new network connections.
Toll pricing

Add mode-specific toll pricing to a selected link in the network.

Data requirements

The TrafficAssignment model requires information about the number of trips to assign (i.e. how much people are traveling by which mode between each location in the study area) and about the network including characteristics relating to speed and capacity per mode.

The required datasets are usually provided by the municipal traffic department or retrieved from a conventional traffic model. If there is no data available, the travel demand can be estimated based on socio economic data and traffic counts. Network data can be generated from public sources such as OpenStreetMap.

Dataset	Description	Format	Common source
Demand	Travel demand contained in OD-matrices. Ideally these matrices are specified per year, time of day and vehicle class and match the zones (TAZ) of the network dataset.	.csv or .txt	Conventional traffic model (e.g. OmniTRANS, Visum, Aimsun)
Network	Network data including links, nodes, zones, turns and junction delays. Ideally the network is loaded with mode specific intensities for calibration purposes.	.cpg, .prj, .dbf, .shp, .qmd or .shx	Conventional traffic model or public resources (e.g. OpenStreetMap)
Road impedance function	BPR or VDF parameters (alpha and beta) per link type.	-	Conventional traffic model

Model architecture

The TrafficAssignment model starts calculating whenever there are changes in any of the data collections to which it is subscribed, for example on the activation of a control in the web interface or output published by other calculation models such as Demand and the NewMM.

Data collection	Description	Input (read)	Output (write)
ROADS	Information about the road network.	Links Nodes Speeds Capacities Link length	Road intensities
TRAF_ZONES	Information about zones.	Zones (TAZ)	-
TRAF_DIMENSIONS	Information about dimensions modeled.	Dimension_id BPR-value	-
TRAF_ODMATRIX	The number of trips between each OD for each dimension.	Trips	Travel times and distances

Parameter	Description
referenceRun	Write all matrix results to the reference columns and shut down the model
writeSkims	Write travel times, distances (and costs if monetaryCosts is set) to the ODMatrices of the defined dimensions
iterationsVolumeAveraging	The number of iterations if VolumeAveraging is used
dimensionsVA	A list of dimensions which should be assigned using volume averaging
dimensionsAON	A list of dimensions which should be assigned using All or Nothing assignment
sumDimensions	Dimensions fow which the intensities should be summed into a single "Derived Intensity" during the calculation
totalLoadDimension	The dimension to which the sumDimension "Derived Intensity" should be written
filterUTurns	Leave out all U-Turns when reading in the network
includeMonetaryCosts	Include monetary link costs in the path costs for assignments
availableGPUMemory	Maximum amount of GPU memory claimed by model
iterationsLUCE	Number of iterations if Luce is used
interpolationMethodLUCE	Interpolation method for Luce if used
AssignmentMethod	Assignment method e.g. VA or Luce

Methodology

The assignment utilizes a static deterministic multi-user-class (equilibrium) assignment and allows to assign modes trough an all-or-nothing and/or volume averaging assignment technique. The all-or-nothing technique assigns traffic between an OD-pair on the shortest path. The volume averaging technique (re)assigns traffic during multiple iterations, with this technique the impact of congestion on route choice is taken into account.

The goal of static traffic assignment is to allocate a given travel demand (a set of trips with fixed origins and destinations) on the transportation network in order to obtain an initial spatial distribution of the traffic volume. Static assignment assumes that the number of trips on a link will be constant during the considered period of time and that all trips will be completed during this period. The resulting traffic volume represents the average conditions for the time period under consideration, making the technique suitable for studying specific periods such as the morning peak hours or an average weekday. A limitation of static assignment is its inability to fully capture dynamics of trip departure and real-time routing behavior with the risks of underestimating congestion levels. In addition, static assignment may result in link volume that exceeds link capacity. In spite of these limitations, static assignment is a valuable approach to traffic analysis as it allows to quickly estimate the use of traffic networks and to develop an initial appreciation of the situation.

The following methods are used within the TrafficAssignment model:

1. BPR function
To determine the travel times between origins and destinations.

2. Dijkstra's algorithm
To determine the shortest path between origins and destinations.

3. All-or-nothing and volume averaging assignment methods
To assign trips to the network.

Travel time function

For computing link travel times Urban Strategy uses the BPR function, which is developed by the American Bureau of Public Roads. It defines the relationship between travel time, volume and capacity in accordance with the following formula:

\[ T = T_0 \cdot \left( 1 + \alpha \left( \frac{I}{C} \right)^\beta \right) \]

where:

\(T\) is the travel time
\(I\) is the intensity
\(C\) is the capacity
\(T_0\) is the free-flow travel time
\(\alpha\) and \(\beta\) are user-defined coefficients

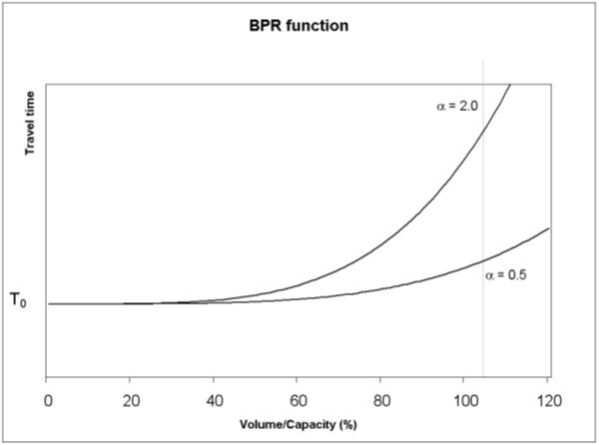
The relationship is as shown in the figure below. In short, \(T_0\) represents a base travel time which is then factored to give a new travel time for a given link. If \(\alpha = 0.5\), delays will occur if the link volume is approaching full capacity (main highways). If \(\alpha = 2.0\), significant delays will occur well before full capacity is reached (residential roads) as shown in the figure below. The function is assumed to simulate the delay occurred in a roadway as a consequence of intensity approaching the road capacity.

Dijkstra's algorithm

Urban Strategy computes shortest paths from a given origin \(S\) using Dijkstra's algorithm (forward search): the length (cost) of a link between A and B in the network is denoted by \(d_{A,B}\). The path or route is defined by a series of connected nodes, A-C-D-H, etc., whilst the length of the path is the arithmetic sum of the corresponding link lengths in the path. Let \(d_A\) denote the minimum distance from the origin of the tree to the node or centroid \(A\); \(P_A\) is the predecessor or backnode of \(A\) so that the link \((P_A, A)\) is part of the shortest path from \(S\) to \(A\). The procedure for building a minimum path tree from \(S\) to all other nodes is described as follows:

Initialization: Set all \(d_A = \infty\) (a suitable large number depending on computer and compiler) except \(d_S\) which is set equal to 0; set up a loose-end table \(L\) to contain nodes already reached by the algorithm but not fully explored as predecessors for further nodes. They are the tip of the tree as branches grow to reach all nodes. Initialize all entries \(L_i\) in \(L\) to zero, and all \(P_A\) to a suitable default value.

Procedure starting with the origin \(S\) as the ‘current’ node is \(A\):

Examine each link \((A, B)\) from the current node \(A\) in turn and, if \(d_A + d_{A,B} < d_B\) then set a new value for \(d_B = d_A + d_{A, B}\), make \(P_B = A\) and add \(B\) to \(L\);
Remove \(A\) from \(L\), if the loose-end table is empty, stop; otherwise,
Select another node from the loose-end table and return to step 1 with it as the current node.

Three comments should be made at this stage. First, routes are in general not allowed to use centroids; therefore in step 1, \(B\) would not be added to \(L\) if it was a centroid. Second, Dijkstra selects the node nearest to the origin, i.e. the node \(L_i\) such that \(d_{L_i}\) is a minimum. This requires some additional calculations (including sorting of nodes using a priority queue) but ensures that each link is examined once and only once. Finally, trees are stored in the computer as a set of ordered backnodes in which \(A\) is the backnode of \(B\) if link \((A, B)\) forms part of the tree.

The shortest route can be determined on the basis of either distance or travel time (including turn delays). Urban Strategy converts these attributes into a generalized cost according to pre-defined weighting factors. It should be noted that in a simple assignment such as all-or-nothing (discussed below), the travel time is a function of distance and travel speed. However, while accounting for congestion, the travel time becomes a function of the I/C ratio, defined by the BPR function.

The basic generalized cost formulation is best summarized by the following equation:

\[ G = \lambda \cdot D + \mu \cdot T \]

where:

\(G\) is the generalized cost
\(D\) is the travel distance
\(T\) is the travel time. This includes static turn delays. In a volume averaging assignment (discussed below) the travel time is determined by the BPR function
\(\lambda\) is the coefficient for distance applied throughout the network
\(\mu\) is the coefficient for time applied throughout the network

Paths built using this Generalized Cost formulation with or without capacity effects are called deterministic as opposed to stochastic (randomized). Urban Strategy does not account stochastic effects in the generalized cost, and thereby in route choice.

Traffic assignment methods

Having built the shortest paths in the network, there are various ways as how the trips can be assigned (loaded) to the network. There is the 'all-or-nothing' assignment which ignores the effects of congestion using just the shortest paths. Volume averaging is a path based method that iteratively assigns the current shortest path taking congestion effects into account. The local-user cost equilibrium method is an origin or bush based algorithm assigning multiple paths towards a single destination in one iteration, hence needing more memory but converging in fewer iterations.

All-or-Nothing (AON)

This assumes that all trips between an origin and a destination take the shortest path as determined by the generalized cost. It also assumes that there are no capacity problems and that this path is perceived by everyone as the shortest path. There are no iterations required.

Volume Averaging (VA)

This assumes that link flows are influenced by existing link flows (hence travel times) and are affected by link capacity. This requires an iterative process by which trips are loaded onto the network and where link travel times are adjusted according to the assignment volume and capacity using a Travel Time Function (BPR function). The objective is to achieve a network wide balance, or equilibrium, between link flows and link speeds (times), taking into account the network capacity. Trips can be loaded onto the network using a volume averaging approach.

In a volume-averaging assignment, also known as the method of successive averages, volumes (demand) are assigned to a network in an iterative process. In the traffic model, the first step in the iteration is always an AON assignment on the shortest route for the demand. The summing of the traffic volumes in the first steps is assumed to simulate the network characteristics of a pre-load situation in the road, including freight, car traffic, etc.

Volume is calculated as a linear combination of the volume found in the previous iteration and the volume added by means of an all-or-nothing assignment performed in the current iteration. By default, in each iteration of a volume-averaging assignment, the fraction \(1/n\) is used to increase the link volume and the value \((1-1/n)\) to reduce it, \(n\) being the number of iterations.

The volume averaging process terminates either when convergence has been detected i.e. when the maximum number of iterations \(N\) has been reached. The number of iterations is user-defined. Effectively when the convergence criteria is reached, we can conclude to a degree of certainty that traffic has achieved a Deterministic User Equilibrium (DUE).

The Volume Averaging method uses the Relative Gap as stopping criterion. When this value is below the threshold, which is usually defined as a small, non-zero value, the assignment will be considered as converged and the assignment will be stopped. The formula for the gap is as provided below:

\[ DG^i = \frac{\sum_a c_a x_a}{\sum_{rs} \pi_{rs}d_{rs} } -1 \]

where:

\(DG^i\) is the duality gap value for iteration \(i\)
\(c_a\) is the cost of link \(a\)
\(x_a\) is the load on link \(a\)
\(\pi_{rs}\) is the optimal cost from \(r\) to \(s\)
\(d_{rs}\) is the demand from \(r\) to \(s\)

The gap \(DG^i\) refers to the flow-weighted difference between current total cost estimates on the network, as determined by the present flow pattern and the speed/flow curves, and the costs if all traffic would use minimum cost routes (as calculated by the next all-or-nothing assignment).

Local-User Cost Equilibrium (LUCE)

The LUCE algorithm is an origin or bush based algorithm which uses an all or nothing assignment as starting point. For each destination, a directed acyclic graph (the bush) is used to assign the trips from all other zones via multiple paths at once to a destination. The bushes are checked and updated every iteration. Moreover, the trips are updated every iteration using a quadratic linear interpolation method per destination.

The LUCE method enables the assignment to spread the trips at multiple paths in a single iteration. This can make the model converge in fewer iterations than e.g. VA. However, this comes at the cost of more memory being used (storing all assigned trips per zone) and the iterations being slower. Hence, a trade off can be made.

Benchmark

Calculation times of the TrafficAssignment model with different datasets and iterations.

Setup	Zones	Links per mode	Modes	Iterations: 5	Iterations: 10	Iterations: 20	Iterations: 30
San Diego County	4.947	42.738	3	00:31,9	00:39,7	00:53,7	01:08,6
Amsterdam cutout	3.035	39.007	3	00:11,4	00:12,9	00:19,5	00:28,9
Amsterdam full	5.460	108.079	3	00:33,0	00:40,9	00:59,1	01:17,4
NL national (LMS)	1.565	112.860	3	00:26,3	00:42,2	01:12,5	01:42,0
Eindhoven Metro*	6.275	174.508	3	00:49,0	01:08,2	01:50,5	02:29,9

*Eindhoven Metro ran with limited memory capacity (24GB). Using sufficient memory capacity (ca. 80GB) would lead to about 1/3 of the documented calculation time.

Literature

For more details on static traffic assignment we refer to the following book on Transport Modelling:

Ortúzar & Willumsen (2011). Modelling Transport, 4th Edition, Oxford, United Kingdom: John Wiley and Sons, Ltd